The Science of Climate Change

JoshNH4H · 2019-02-09 14:51:23

I have said repeatedly that nonuniform temperature lowers the mean temperature of a planet, all else being equal. As an addendum to the previous post (#150) I want to go through the math of that here so that you all can see what I mean.

For this post, I will be using the Moon as an example because it is the Moon where this is clearest.

For simplicity's sake, I will be modifying the UTSA as follows:

Assuming that a planet has a day side and a night side, each of which is uniform in temperature and covers 50% of the surface area of the planet and assuming that the difference in temperature between the two sides is by an amount D. As a result, the P_out equation is modified in the following way:

P_out=2*ϵ*σ*π*r^2*(T-D/2)^4+2*ϵ*σ*π*r^2*(T+D/2)^4

T here is the mean temperature of the planet averaged based on area; It is exactly halfway between the day and night temperatures.

Previously I calculated the UTSA temperature of the Moon to be 274 K.

Assuming a 150 K difference between daytime and nighttime temperatures, this nonuniform model finds an average temperature of 250 K--24 K lower than a uniform model and just 10 K higher than the actual observed lunar mean.

At 274 K the entire surface of the Moon will radiate at 318 W/m^2, which is the correct value for the energy balance to work out. However, with the nonuniform model things are different. If the mean temperature remained at 274 K with half the Moon 75 K higher (349 K) and the other half 75 K lower (199 K) the day side would radiate at 841 W/m^2 and the night side at 89 W/m^2. Averaging out, the Moon would radiate at 465 W/m^2. This is higher than the energy received (1366*(1-0.07)/4) W/m^2 or 318 W/m^2 and therefore it will cool until equilibrium is reattained.

What happened here is that when the daytime and nighttime temperatures diverged, daytime emission rose faster than nighttime emission fell and as a result total emissions were higher.

This is why temperature nonuniformity lowers mean temperature; It's also one of the two reasons why Venus's mean temperature is higher than Mercury's even though it's twice as far from the sun and has a much higher albedo.

SpaceNut · 2019-02-09 17:36:27

Part of the dynamics comes from earths oceans versus land area and not just its atmospheric make up.
190206-ocean-color-climate-change-ac-602p_00d48e93256d83182c410fbd93710345.fit-760w.jpg

climate change will affect the ocean's color

By 2100, the color shift could affect more than 50 percent of the oceans’ collective 140 million square miles of surface area. Rather, it's that populations of marine phytoplankton will fall as seawater warms. Since these tiny organisms contain the green pigment chlorophyll, any change in their numbers affects the water’s apparent color.
The shift could be ominous because phytoplankton serve as a food source for small sea creatures that, in turn, are eaten by fish, squid and shellfish. If phytoplankton populations dip too low, vital fisheries in certain areas could be decimated.
A report published in December 2018 by the Global Carbon Project showed that after a brief period of stability from 2014 to 2016, global greenhouse gas emissions started rising sharply. Thus the global temperature rise might exceed 3 degrees Celsius by the end of the century, triggering an even more dramatic effect on phytoplankton.

kbd512 · 2019-02-09 17:55:15

Josh,

In the past, you've said you won't discuss perpetual motion machines. As near as I can tell, this supposed "greenhouse effect" is a thermodynamic perpetual motion machine. I've been trying to figure out how it's different from a perpetual motion machine, to no avail. I'll rely upon your expert knowledge to set me straight. We seem to get twice as many watts of energy out than were input to begin with. Maybe there's something about this "simple model" of the "greenhouse effect" that I don't understand, but you've said I lack a basic understanding of this, so I'm deferring to you to explain to the rest of us how this works.

Could you please explain how NASA's Dr. Gavin Schmidt learned from this simple model that we could double the amount of energy out, via the "greenhouse effect", that was received as input from the Sun to begin with?

Note: if the formatting doesn't come through, then I'll edit this post

Learning from a simple model

Edit: HTML formatting didn't come through, so this is about as good as I can do here:

G = σTs^4 = S/(1-0.5λ)

G - greenhouse effect
σ - Stefan-Boltzmann constant
Ts - surface temperature
S - solar radiation (Watts per square meter)
λ - emissivity

If λ = 1; 240W/(1 - 0.5λ); 240W / 0.5 = 480W

If λ (emissivity) equals 1, then how do we get 2 units of output energy from the 1 unit of input energy?

Does this work anywhere else in thermodynamics, or does it violate the 1st law of thermodynamics?

I just want to know where all this additional energy came from. It clearly didn't come from the Sun, so where did it come from?

I've seen the diagram and explanation in numerous texts regarding climate science, as it pertains to the greenhouse effect, so if it's not a widely held belief then I'm not sure why so many different universities teach it.

Last edited by kbd512 (2019-02-09 17:59:44)

SpaceNut · 2019-02-09 18:30:11

NASA and others have a collected recording of temperatures for 134 years, and 15 of the hottest years they’ve measured have been since the year 2000.

Although such a small rise in temperature seems inconsequential, the problem is that it doesn’t get spread out evenly. Some countries could experience warming on a scale of about 5 to 10 degrees – a substantial increase which could pose a threat to agriculture, wildlife, and life in general.

The US, carbon dioxide accounts for about 80% of all greenhouse gases, with methane, nitrous oxide, and industrial fluorinated gases making up the last 20%. These gases mostly come from burning fossil fuels for energy and transportation as well as industrial processes, agriculture, and home use (heating and cooking). Even clearing forests to mine for these energy sources and transporting them to where they are needed contributes to the problem.

Our requirement for electricity has caused use of nuclear fueled plants that require cooling via the water source that its located near as well for an input to earths warming.

http://solar-center.stanford.edu/sun-on … -warm.html

Global Warming vs. Solar Cooling: The Showdown Begins in 2020

GW Johnson · 2019-02-09 23:17:55

Kbd512:

My version of Josh’s simple UTSA model works very simply. Like what Josh said, power-in equals power-out, implying steady state, as well as energy conservation.

Power-in is the power per unit steradian received at the Earth from the sun (basically the source of the solar constant at Earth’s distance from the sun). The projected area of the Earth in the direction of the sun from which the power comes, is a flat circle of area A = pi R^2.

There’s some 2 pi factors here and there for the steradian solid angle stuff, but the basic notion is power/unit area times area equals the power input to the Earth just outside its atmosphere. Because the atmosphere is transparent to visible wavelengths, you multiply the exoatmospheric solar input by 100% transmissibility to be the power actually striking the surface.

Some of that power striking the surface is visible wavelength power reflected back into space, but the bulk of it is absorbed and re-emitted as infrared radiation (IR). This happens throughout the entire 4 pi steradians of solid angle, which is why the IR radiating area is Earth’s surface area 4 pi R^2, not the projected flat circle area pi R^2. It radiates to 4 K cold space.

The radiated infrared calculates from the power/area = Boltzmann’s constant x emissivity x surface temperature ^ 4. In the simplified UTSA model Josh describes, we assume the entire surface is of uniform average temperature. This ignores day/night variations, latitudinal variations, and weather-related variations. (And a lot of other things, too. Modelling all that stuff is what climate models try to do, in different ways, and with differing results.)

This average surface temperature governs the radiated infrared. The reflectance of the surface times the solar power received, governs the visible power reflected back into space. Its emissivity is 1 – reflectance. The independent variable here is the value of the average surface temperature. It takes on the value that makes power-in equal to total power-out. THAT is equilibrium.

The atmosphere is not perfectly transmissible to infrared. Some is “lost” to local absorption in the air. That raises the surface power required to achieve overall equilibrium (a higher surface emission x less-than-100%-transmissibility = net radiated infrared that reaches space).

Thus ANYTHING that reduces atmospheric infrared transmissibility raises the surface temperature required to reach equilibrium. Because of the temperature^4 variation, this balance is VERY SENSITIVE to small changes in infrared transmissibility.

Obviously this model is way-over-simplified, but it gets the point across. The trends are the real point with it.

There is no extra energy coming from anywhere in this model. What goes in, comes out. Period. Steady-state energy conservation. But, the ease with which the IR portion gets out, governs the equilibrium surface temperature. That “ease” is the IR transmissibility of the atmosphere.

Gases in the mix that are less transmissible to IR reduce the transmissibility of the mixture, and thus raise the average equilibrium temperature. That long-winded sentence IS a description of the “greenhouse effect”.

GW

Last edited by GW Johnson (2019-02-09 23:24:56)

SpaceNut · 2019-02-10 10:51:27

To have a change of temperature that effects earth in general means something is changing with obsorbtion. We know that Ice gets dirty so it obsorbs more, the water causes seas to rise, with what seems a wobble of the poles to change earths tilt, releasal of co2 happens from the ice melt and change of ocean salinity, we get rain that errodes the green area of the earth causing a drop in oxygen creation which continues the co2 level build up, Earth tilt change will cause more ice melt and other areas to be effected by the excess heat of summer... as we see its a snowball effect what is occuring....

GW Johnson · 2019-02-10 11:55:56

Hi Spacenut:

I saw the "snowball effect" you speak of, first-hand on a small scale during those winters I spent in Minnesota decades ago. It's real.

In the fall, it would snow-and-melt, repeatedly, without covering the ground in white. Then would come the snow that wouldn't melt, immediately crashing temperatures colder by 10-20 or even more degrees.

It would stay that way, much colder, until finally just enough snow ablated for the dark ground to begin appearing. Almost immediately, temperatures would suddenly and dramatically rise, and the snow would all melt away in a couple of days.

It operated like a switch: flip-flop. Hot then cold. Cold then hot. Nothing about this was gradual. Not at all.

GW

kbd512 · 2019-02-10 13:50:34

GW or Josh,

Can you tell me where those extra watts of power came from, as it pertains to Dr. Schmidt's equation from the link I provided, entitled "Learning from a simple model", from Post #153?

Dr. Schmidt, of the NASA Goddard Institute for Space Studies (GISS), used that equation to explain the greenhouse effect. So far as I know, Dr. Schmidt is a real climate scientist. Perhaps he's not the world's greatest physicist, but who knows, as I'm neither of those things. I didn't pull that equation out of my rear end for sake of argument. As indicated in Post #153, what I did do was quite simple. I actually used Dr. Schmidt's equation. I plugged in 240 watts of power from the Sun (the number that Dr. Schmidt used in his example in the link I provided), I set emissivity equal to 1 (for maximum "greenhouse effect"), and the result was 480 watts of power out. I've either recently become incapable of simple math, or something is clearly missing from Dr. Schmidt's "greenhouse effect" equation.

If energy is conserved, then where does that much extra power come from if the "greenhouse gases" in Earth's atmosphere acts like a perfect LWIR mirror?

Was Dr. Schmidt's "greenhouse effect" equation over-simplified in some way, for explanatory purposes?

Was some other factor not included in order to convey the idea of the "greenhouse effect" concept?

In the article Dr. Schmidt stated that this concept is pretty simple, even if there's a little math involved and, as you've already noted, other factors that govern precisely how much power is transmitted from the Sun to begin with because Earth is a half-irradiated sphere.

So, what am I missing?

Why can't the energy industry use this supposed "greenhouse effect" to our advantage?

Why can't I shine a flashlight or laser on a mirror and double the beam power that the flashlight or laser was capable of producing to begin with?

Getting 2 watts of power output for every watt of input power, by injecting CO2 or some other IR opaque gas into a chamber surrounding an IR laser, sounds like a pretty good deal to me. If this "greenhouse effect" doesn't work anywhere else in the application of thermodynamics, then it is rather odd that it was used by an expert in climate science to explain that effect. It looks like a blatant violation of "settled science", or at least the 1st law of thermodynamics- perhaps controversial amongst climate scientists but apparently unassailable for power plant engineers, but anyone here is free to point out where I'm wrong.

Since we now have IR lasers that are over 80% efficient (wall-plug to emitter), if this "greenhouse effect" is real we should be able to produce IR laser electrical power plants that run themselves after some power is initially expended to start up the power plant. I think you both intuitively know that that's impossible. Something has to give. Dr. Schmidt either provided a wildly inaccurate mathematical equation to demonstrate the "greenhouse effect", the "greenhouse effect" doesn't work the way his equation indicates, or the 1st law of thermodynamics is incorrect.

JoshNH4H · 2019-02-10 14:05:36

In response to kbd512's post, #153:

If you want to split hairs, my recollection (I could be wrong!) of what I have said is that I have no interest talking about cold fusion. Regardless, you are right that I wouldn't bother talking to someone pushing a perpetual motion machine. The common thread between the two is that it's generally not worth my time to engage with the (often conspiracy-minded) people who will reject scientific consensus in favor of their own unsupported (and usually easily disprovable) nonsense.

It is for precisely this reason that I typically avoid engaging with climate change denialists. I have relaxed that rule in this case because I respect your intelligence. I can't say I've gleaned any benefit from doing so, but here we are.

Your question, as I understand it, is this: How can it be the case, if absorbed sunlight averages 240 W/m^2 over the surface of the Earth, that the Earth's emissions can be double that at 480 W/m^2?

Your question "Is this not a violation of the conservation of energy?" seems particularly strange in context, because the analysis on that page is based entirely on the conservation of energy.

I notice you made an error in defining your variables. You said "G - greenhouse effect". But this is not right. G in this case is for "Ground"--the G-term refers to thermal emission by the ground. The A-term is in fact the one more closely associated with the greenhouse effect.

Likewise the term λ is a bit more complicated than just the emissivity/emittance of the atmosphere. An interesting fact about emittance and absorbance is that (for the same angle of incidence if the material is solid) they are the same value at the same wavelength.

On the whole, I believe the page you linked does an excellent job of explaining a simple equilibrium model for the greenhouse effect. I'm not sure that I can explain it better or differently but I will try. Please excuse the poor quality of my graphics.

In this first image, I look at the energy balance of the ground, the atmosphere, and free space. "Free Space" can be considered to be a control volume that encloses the whole universe except for the Earth and its atmosphere. For each of the three control volumes (ground, atmosphere, and free space) the energy input equals the energy output.

Then in the following image I created a sort of flow chart with equations. In the webpage you linked to, S equals the energy absorbed by the Earth's surface; They ignored albedo effects by reducing S to the correct value. I have followed that convention below.

Another way of explaining the answer to your question is to consider two parallel mirrors with a beam of light bouncing back and forth between. The beam itself may have a power of 1 watt; but if it bounces back and forth 100 times between the mirrors you will find it to be the case that a control surface has 100 W of light passing through it in each direction. It's not a violation of conservation an energy, just a consequence of comparing apples to oranges and looking at the wrong control surfaces and volumes. The model presented in that webpage is mathematically analogous to a mirror which is partially reflective and partially transmissive (with a stipulation that it can be no more than 50% reflective because emissions go in both directions).

Hope this helps

kbd512 · 2019-02-10 17:07:09

Josh,

So far as I know, measuring a 1 watt beam of light 100 times doesn't make it possible to obtain 100 watts of continuous power from that beam of light. After 1 hour of time has elapsed, 1 watt-hour of power was transmitted from the emitter source. It makes no difference how many times you measure it, nor how many times that 1 watt of power is reflected, because there's still a maximum of 1 watt of power in the beam and the maximum amount of thermal energy that the beam could deposit into something it strikes is 1 watt. I would then also think that incoming radiation striking the surface of the Earth with 240 watts of power can't result in all 240 watts of power being simultaneously reflected back out into space and re-radiated back to the surface of the Earth, presuming that CO2 / CH4 / NOx molecules re-radiate or scatter emitted radiation in all directions. That was the part I didn't understand.

Apologies. I did make a mistake when labeling my variables. I noticed that the atmospheric equation was equal to "λG". If λ was 1, that was equivalent to the surface emission. That didn't make much sense to me, much like the doubling of the effective power, so I just labeled it the "greenhouse effect".

SpaceNut · 2019-02-10 18:10:11

Solar is not as we see the only energy input for what we are call global warming aka climate change as we do get internal releases of energy from inside the earth in lava flows.

http://www.msn.com/en-us/video/science/ … vi-BBTk2mA

There is also input from the gained co2 entering the earth atmospher from other sources that were given that energy from the solar wind as earth sweeps its path around the sun.

JoshNH4H · 2019-02-10 20:20:53

kbd512 wrote:

Josh,
So far as I know, measuring a 1 watt beam of light 100 times doesn't make it possible to obtain 100 watts of continuous power from that beam of light. After 1 hour of time has elapsed, 1 watt-hour of power was transmitted from the emitter source. It makes no difference how many times you measure it, nor how many times that 1 watt of power is reflected, because there's still a maximum of 1 watt of power in the beam and the maximum amount of thermal energy that the beam could deposit into something it strikes is 1 watt. I would then also think that incoming radiation striking the surface of the Earth with 240 watts of power can't result in all 240 watts of power being simultaneously reflected back out into space and re-radiated back to the surface of the Earth, presuming that CO2 / CH4 / NOx molecules re-radiate or scatter emitted radiation in all directions. That was the part I didn't understand.

Hey kbd512,

Probably the key point to understand here is that the 480 W includes both sunlight being absorbed by the ground and sunlight being re-radiated back at the ground by the atmosphere. If you're willing to put up with more crude MS Paint drawings, it's easier to show than tell.

What I have drawn here is an idealized 1 W laser pointed at two parallel, idealized, perfectly reflective mirrors, reflecting several times, and striking a calibrated detector. I have chosen this setup because it is strongly analogous to (Although not strictly identical) the situation described in the webpage you linked to. The system is assumed to be at equilibrium.

The input to the system is 1 W of unidirectional laser light, which reflects three times each off the top and bottom surfaces until it is received by the detector, which measures 1.0 W of output light.

It's not something you could measure physically, but I'm sure you will agree that in this scenario there are actually 3 W of power striking both the top and bottom mirrors at any given time. This doesn't violate conservation energy because it's the same energy, bouncing back and forth until it's absorbed by the detector. For 1 W of power, the detector probably does not need to be cooled, but if it were instead a 100 or 1000 W beam the detector would presumably have some way to dispose of that heat.

Now consider the following scenario, which parallels the model shown in the website you linked. I have followed their convention of ignoring the albedo of the Earth. Therefore, instead of showing 1366/4=340 W/m^2 of sunlight with 100 W/m^2 reflecting immediately back into space as visible light, I have shown 240 W/m^2 of sunlight that is absorbed 100% by the ground.

For the purposes of this post, I will use λ=2/3.

We know starting off that A=240 W/m^2 because that's an external limit.

We know that B=A+D, from conservation of energy.

We know that A=C+E, from conservation of energy.

We know that C=(1-λ)B [Note 1]

We know that B=σTg^4 from the Stefan-Boltzmann law (with the assumption that the emittance of the ground is equal to 1; Tg is the temperature of the ground).

We know that D=E=λσTa^4 [Note 1] because it's an assumption of the model (the key simplification in this model is treating the atmosphere as a uniform temperature layer over a flat planet; Ta is the temperature of the air)

So: We have a system of four equations with four unknowns.

Eq 1: B=240+D
Eq 2: 240=C+E
Eq 3: C=1/3 B
Eq 4: D=E

I am confident you can solve these for yourself and will simply present the answers below. But before I do that I want to direct you to equation 1, which is the energy balance for the ground. Because λ=2/3 (and for any real atmosphere that is not a hard vacuum λ is greater than 0) and because T is necessarily greater than 0, we know that D>0. Therefore, B>240 (B>A). Basically what's happening is that radiation is bouncing around between the ground and the atmosphere in a similar manner to the first image I posted [Note 2]. Without further ado, the values for each is as follows:

A=240 W/m^2
B=360 W/m^2
C=120 W/m^2
D=120 W/m^2
E=120 W/m^2

And we can therefore calculate that Tg=282 K and Ta=237 K.

I want to point your attention to two more things before I wrap up:

First, on the page you linked, they used λ=.769 to calculate Tg=288 K, which corresponds to the actual, measured ground temperature of the Earth. In this model, I used λ=.667 and calculated Tg=282 K, 6 K lower. T=287 K (the preindustrial global mean) implies λ=0.740, which seems like a difference commensurate with a near-doubling of the second-most important greenhouse gas.

Second, that this model is great for helping to understand the radiative insulation effect of an atmosphere but fails to approximate reality in one extremely important respect. I have mentioned it already, but the atmosphere is not just a single layer with a single value for its absorbance/emittance. It's an infinite number of infinitesimally small layers, each with its own differential value for absorbance and emittance. You pointed out that λ=1 (the maximum mathematical value) implies B=480 W/m^2. I will go one step further and point out that B=480 W/m^2 implies Tg=303 K, a hot day but certainly something that you experience. If you were to give Earth a Venuslike atmosphere, the Tg would certainly be higher than this. The point is that this model likely understates the marginal effect of marginally higher atmospheric absorbance to some degree. Incidentally it would be a very good model for an actual greenhouse.

I hope this has helped.

Note 1: There is an assumption here that is basically reasonable for a simple model but I think is worth mentioning. I said before that at a given wavelength, absorbance=emittance. This is true. Because the blackbody spectrum is a function of temperature, absorbance=emittance is a good approximation for the atmosphere as long as it's at a close-enough temperature to the ground that the spectra are similar. As the temperatures diverge absorbances and emittances will diverge in ways that are hard to predict without a more powerful model. For reference, using my calculated values for Tg=282 K and Ta=237 K, the wavelength with the most emission is at 10.3 μm and 12.23 μm respectively. This is a simplified and imperfect model which I believe nevertheless captures several important dynamics of the greenhouse effect.

Note 2: It happens to be the case that thermal absorption and re-radiation is not as different at an atomic scale from mirror reflection ("Coherent Reflection") as you might think.

JoshNH4H · 2019-02-10 23:07:55

As a very brief follow-up to the previous post, for λ=0 the model simplifies to the UTSA model I discussed earlier.

SpaceNut · 2019-02-11 17:26:45

The sun produces non focussed light which can vary quite a bit around its mighty size with drops with sunspots that drop its output but it depends on alignment of the spot to earth. A laser creates focused culminated light so they are not quite the same in source.

JoshNH4H · 2019-02-11 18:46:46

Hey SpaceNut,

As I said in the post the laser/mirror setup is analogous but not identical to the model of the greenhouse effect presented on the RealClimate website linked to by kbd512. The key similarity is the energy flows. Naturally the sun is a substantially different light source than a collimated laser.

SpaceNut · 2019-02-11 19:11:38

It does allow for the testing of the amounts for the atmosphere which can obsorb and at the rate to which it can.

kbd512 · 2019-02-12 14:04:27

Josh,

First, thanks for the explanations.

Second, does the "simple model" from the explanation given by Dr. Schmidt require the use of a time component, or is that not required since half of the Earth's surface is continuously exposed to the radiation from the Sun?

Let's say I want to boil a cup of water using my IR laser and a CO2 filled polished stainless steel (idealized reflector; I know it's not and we'd probably have to use some other specialized materials to get this to work as envisioned, but work with me here) thermos (laser fires into the gas cavity to heat the CO2 such that all the emitted power is absorbed by the CO2). Instead of the walls of the thermos containing a hard vacuum, this thermos is filled with CO2 to maximize the greenhouse effect. My IR laser emits 10 watts of power. With this setup, can I get 20 watts of heating power from my IR laser?

Ignore the efficiency of the laser for a moment and pretend that it only emits radiation in the frequency bands that the CO2 can absorb. My only goal here is to heat my cup of water for my morning coffee faster. With the right equipment / setup, can I use the greenhouse effect feature of CO2 to surround the water with an effective 20 watts of power, or do I still just get 10 watts of power from the laser (the maximum amount of power my laser was capable of continuously emitting)?

If I only get 10 watts of power, then I'm still not completely clear on how that system of equations conserves energy. If the greenhouse effect works in the atmosphere to produce a combined 480W of power (edit: when λ = 1), through whatever mechanism, from the 240W that's continuously going in, then concentrating the CO2, or any other IR opaque gas for that matter, should boil my water faster, right?

If I get 20 watts of power, then have there been any experiments to see if we can use this effect with a solar power tower to increase thermal power transfer to a molten salt, such as a CO2 filled double-wall doped quartz crystal salt vat that lets SWIR from the Sun in, but traps all or most of the emitted LWIR going out?

Last edited by kbd512 (2019-02-12 17:08:17)

SpaceNut · 2019-02-12 18:46:00

The heliotowers use several mirrors that reflect to a common spot to generate the heat wattage on a target area and passes through the atmosphere for each I am sure with some loss. The concentrate light is culminate to the spots focus area.

The experiment is different but if the area of the beam is spread out then its a surface area of obsorbtion and should be just 10 w of energy minus losses.

JoshNH4H · 2019-02-12 23:38:07

Hey kbd512,

I’m always glad to share knowledge when I have knowledge to share.

kbd512 wrote:

Second, does the "simple model" from the explanation given by Dr. Schmidt require the use of a time component, or is that not required since half of the Earth's surface is continuously exposed to the radiation from the Sun?

There are a number of ways I can respond to this, all of which are unsatisfying in some respects.

The first is tautological: This model does not include a time component, therefore a model with a time component would be a different model.

The second is semantic: Because this model does not include a methodology for measuring or calculating λ from other known quantities (the composition and pressure of Earth’s atmosphere, for example) it isn’t really a model at all so much as a learning tool to help understand the greenhouse effect or to analyze the approximate effect of changing certain basic parameters. Therefore trying to use it to model the actual Earth would be to mistake its purpose.

The third is logistical: This model has many flaws as a climate model. Time invariance is one and spatial invariance is another, and treating the atmosphere as a single uniform layer is a third. Of these, addressing time invariance is the hardest and also (possibly) the least significant because you need to think very carefully about how the heat capacity of the various layers of Earth’s thermal system act and interact through all three modes of heat transfer (If you don’t, you’ll get a nighttime temperature estimate of 0 K). It makes more sense, in my opinion, for a research effort to try to address the other two first because you’ll get a better return on your labor.

Hopefully by taking these three answers together you understand holistically what my response is. We went into this acknowledging that the model is simple and limited and time invariance is certainly one of its flaws. We have been working around this by using the “hack” of mean insolation levels, which is reasonable but imperfect. By addressing this and other issues we could build a better and more reliable model.

Now, to go into your thought experiment. I find it always helps to draw a picture, so here's mine:

Here are the assumptions for this model, which I believe accord with the scenario you have described:

Yellow is CO2
Blue is water
CO2 and H2O are completely opaque to thermal radiation
The gray exterior does not allow any heat energy to enter or leave, or alternatively it perfectly reflects that thermal radiation right back into the CO2
Laser light with a power of 10 W enters through an infinitesimally small opening and is completely absorbed by the CO2

Your question is: What happens?

I want to start off by saying that there is no way to do an equilibrium calculation for this scenario because heat is entering and not leaving. In effect, the parameters you have given are non-physical. You have already recognized this and we can still analyze it, but to the extent that the results seem nonphysical it's because the inputs themselves also are.

I'm going to introduce a couple more assumptions so that I can put actual numbers on things:

First, that the mass of the water is 239 g. I have chosen this because, at a heat capacity of 4.184 J/g-K, it will take 1000 J to raise its temperature 1 degree (it's conveniently also just about 1 standard US cup of water). I will assume that the CO2 has a negligible thermal mass in relation to the water and in relation to the power of the laser. I will assume that the water-CO2 interface has a surface area of Ai=100 cm^2 (0.01 square meters) and that the CO2-container interface has an area of Ac=1000 cm^2 (0.1 square meters). I will assume that both the CO2 and the water are at uniform, different temperatures but begin at 0 C. I will assume that heat transfer is only through radiation.

How long will the water take to boil? You might naively say: ΔU=Cp*m*ΔT (Eq. 1), where "U" is increase in energy (in this case as heat), Cp is the specific heat, m is the mass, and ΔT is the change in temperature. I have chosen m so that the product Cp*m=1000. If the temperature difference is 100 K, total energy is 100,000 J and it will therefore take 10,000 s (a bit under 3 hours).

This answer is correct, and I will use the rest of this post to explain why and how.

The analysis in this post is based fundamentally on the first law of thermodynamics. In words, the first law of thermodynamics is conservation of energy, but it has been formalized in a form that can be used directly for analysis. This form is:

ΔU=ΔH-ΔW (Eq. 2)

Where H is enthalpy (heat entering or leaving, with the sign convention that heat entering is positive), W is mechanical work done (work having the technical meaning of FΔx, force times distance, or equivalent), and U is a quantity known as internal energy. Alas, while I am quite comfortable talking about how heat moves I have a much harder time talking about what heat is. Internal energy is a measure of the amount of energy stored in other sorts of forms, including molecular vibration (heat) but also chemical potential energy, etc.

While Eq 2 does hold for the entire universe taken as a system, it's much more useful analytically to cut a slice out of the universe and analyze it independently. There are two approaches to this, "Control Mass" and "Control Volume". If you do your analysis correctly, each will give identical results to the other. Typically, you will choose the one that is easiest to use for the problem you are looking at.

In the control mass approach, you look at a control mass--a particular set of atoms--and see how they change under the influence of whatever conditions they experience. In the control volume approach you define a volume (defined by a surface through which heat and/or matter can enter or leave) and you look at the flux of various quantities through that surface.

This is a great control mass problem, which is good because the control mass approach tends to be more intuitive when you can apply it.

I will define two control masses: The water and the CO2.

Let's look at the water first:

ΔU=ΔH-W

Because the water is neither being compressed nor expanding by an appreciable amount, the work done is zero. Therefore we have ΔU=ΔH

ΔH is equal to the heat entering (Ew) minus the heat leaving the water (Lw). ΔU is as in Eq. 1. Therefore we have the following equation that is valid for the water:

Cp*m*ΔT=Ew-Lw (Eq. 3a)

I will return to this later, but first I would like to derive a comparable equation for the CO2 gas.

ΔU=ΔH-W

It is normally unavoidably the case that gases do work when they are heated, either in increasing pressure at constant volume or by expanding at the same pressure (or a bit of both). In a more realistic scenario I would want to include that in my model; in an equilibrium scenario it would be irrelevant because the temperature would not be changing. In this scenario I am going to ignore it. I don’t think this is the property of CO2 you’re trying to get at and it adds unnecessary complication. For the purposes of this calculation it is as if CO2 is a solid with the optical properties you have specified. Therefore W=0.

I stipulated in my assumptions that the thermal mass of the CO2 is negligible. What this means is that the product Cp*m ≈ 0. Therefore:

ΔU=Cp*m*ΔT=0*ΔT=0

And we have:

ΔH=0=Ec-Lc (Eq. 4a)

Where Ec is the energy entering the CO2 and Lc is the energy leaving the CO2.

Going back to equation 3: The energy leaving the water is thermal emission from its surface, and the energy received is the thermal emission from the surface of the CO2. Note that emittance is equal to 1 in all cases and therefore has been ignored. We have:

Cp*m*ΔT=σAiTc^4-σAiTw^4 (Eq. 3b)

or, filling in:

1000ΔT=.01σ*(Tc^4-Tw^4) (Eq. 3b)

Now, for the CO2 it’s a bit more complicated. Energy leaves via thermal radiation towards the wall and towards the water. It’s received by thermal radiation back from the wall, thermal radiation from the water, and from the laser. Plugging in:

0=10+AiσTw^4+AcσTc^4-AcσTc^4-AiσTc^4 (Eq. 4b)

The first term is the laser power, the second emission from the water, the third reflection from the wall, the fourth emission towards the wall, and the fifth emission towards the water. Terms 3 and 4 cancel each other out; removing them and plugging in:

0=10+.01σTw^4-.01σTc^4 (Eq. 4b).

Rearranging:

10=.01σ*(Tc^4-Tw^4) (Eq. 4b)

We see the right sides of Eq. 3b and Eq 4b are equal to each other; and solving for ΔT we find:

ΔT=0.01 K/s (Eq. 5)

Which corresponds to the initial “naive” result.

What actually happens? Initially, the water and CO2 are at equilibrium at 0 C. The water radiates 3.15 W at the CO2; The CO2 radiates 3.15 W at the water and 31.5 W at the wall which is reflected back onto itself. All told, 34.65 W are falling on the CO2 but because it also emits 34.65 W the temperature does not change.

Then the laser turns on. Because the CO2 has no thermal inertia it cannot hold any of the heat and heats up rapidly. Soon, it has reached a temperature of 117 C while the water is still at 0 C. At 117 C (390 K) it radiates much more: 13.15 W at the water and 131.5 W at the wall. The water, which is still at 0 C, absorbs 13.15 W and emits 3.15 W and therefore absorbs a net energy of 10 watts.

This continues for 10,000 seconds (per our calculation) until the water is at 100 C. The CO2 is now at a temperature of 166 C. At 166 C it emits still more: 20.98 W at the water and 209.8 W at the wall. The water, whose emissions have also gone up, absorbs 20.98 W and emits 10.98 W and therefore absorbs a net energy of 10 W. Because of the fourth-power law, the CO2’s temperature has gone up by 49 C while the water has gone up by 100 C.

Once the laser is turned off, the CO2 rapidly cools down to 100 C. The water is still at 100 C and radiates 10.98 W at the CO2; The CO2 radiates 10.98 W at the water and 109.8 W at the wall which is reflected back onto itself. All told, 120.78 W are falling on the CO2 but because it also emits 120.78 W the temperature does not change.

I’ve gone on for almost 2000 words in this post and, though I showed how I would analyze the problem you presented, I’m not sure how much I’ve done to clarify things.

If I had to extract a few key points, it would be these:

Blackbody radiation is everywhere, literally all around us all the time, and is an omnipresent feature of matter in the universe
Most often nearby objects are near thermal equilibrium and the thermal radiation going in one direction cancels out the radiation going in the opposite direction
Just because there is a significant amount of power bouncing around in the form of microwaves does not mean that you could actually use it for anything. Consider the equation for carnot efficiency, which I believe is derived directly from the second law of thermodynamics: Efficiency=1-Tc/Th. You generate energy from thermal gradients and not from temperature itself. Meanwhile thermal radiation is close to omnidirectional, meaning that no possible system of mirrors or lenses could concentrate it to a higher power.

JoshNH4H · 2019-02-13 00:18:49

As far as playing with emittances there are some things you can do, which we do where we can. The simplest of these is to heat something up by painting it black or cool it by painting it white. This changes the portion of sunlight absorbed by an object.

You can also play with emittances; a polished and reflective copper or aluminium surface will emit much less than a rough or painted one, but it will also absorb less. If you're looking at power generation most of your heat losses should be directly into your working fluid (This isn't actually a "loss" at all). We have lots of ways to make that happen, depending on where your energy is coming from and what you're trying to do with it. My understanding (which could be wrong) is that it's not uncommon for concentrated solar power plants to use glass around their working fluid pipes to emulate a greenhouse effect. Normally, you would just use regular insulation and paint it either white or use that silvery-coated stuff, but if light needs to get in you need to get creative.

elderflower · 2019-02-13 03:51:44

Josh
You have used Cp for your CO2 specific heat. There is nothing in your system which will allow free expansion of the CO2, or indeed any expansion. You should therefore have used Cv. The CO2 then stores energy as its pressure increases. Although it makes little difference over 1 degree C, it would be considerable over 60 degrees.

JoshNH4H · 2019-02-13 09:10:45

Hey Elderflower,

I also assumed that Cp*m=0. For a more rigorous model you would be completely right but for this one whether the gas is contained at constant volume or permitted to expand at constant pressure is (if you'll pardon the pun) immaterial

SpaceNut · 2019-02-16 22:34:57

Climate change: Scientists tap nature, space and society

The shrinking rain forest

Understanding Carbon Cycle Feedbacks to Predict Climate Change

Ice volume calculated anew

Climate change is causing glaciers to shrink around the world. Reduced meltwaters from these glaciers also have downstream effects, particularly on freshwater availability. A lack of meltwater can greatly restrict the water supply to many rivers, especially in arid regions such as the Andes or central Asia, that depend on this water source for agriculture.
international team of glaciologists used a combination of different numerical models to calculate the ice thickness distribution and the ice volume of some 215,000 glaciers around the world. The researchers excluded sea ice and glaciers that are connected to the Greenland and Antarctic ice sheets from their calculations.
According to the study, the combined ice volume of all considered glaciers currently amounts to some 158,000 cubic kilometres (km3). The last available estimate - dating a few years ago - was around 18 percent higher.
The largest glacier ice masses (some 75,000 km3) are found in the Arctic and account for almost half of the global glacier ice volume.

Research Paper

SpaceNut · 2019-02-17 18:59:28

Undersea gases could superheat the planet

These undersea carbon reservoirs largely stay put unless perturbed, but the new study shows the natural reservoirs are vulnerable in a warming ocean and provides proof the Earth's climate has been affected by rapid release of geologic carbon.
The scientists say it occurred in the distant past when the Earth was much warmer, and it's happened more recently - about 17,000 years ago at the end of the Pleistocene epoch when glaciers advanced and receded, which is the focus on the new study. Warming was evident due to changes in atmospheric greenhouse gas concentrations, based on ice cores, marine and continental records.
deep-ocean carbon reservoirs are being discovered. They mostly occur near hydrothermal vents, of which scores have been identified so far, especially in the Pacific, Atlantic and Indian oceans. They occur where the Earth's crust spreads or collides, creating ideal conditions for the formation of deep-sea carbon dioxide reservoirs.

Research paper

SpaceNut · 2019-02-18 19:41:19

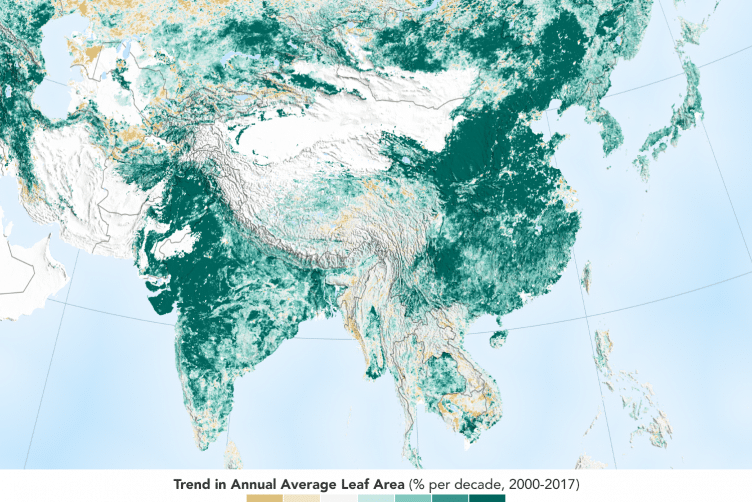
Earth has more green area, but that’s not quite good news

NASA’s satellites, we’ve discovered that over the last two decades, the Earth has increased its green leaf area by a total of 5 percent,

That means we are out putting more than our forests can keep up with.

Each year, about 10 to 11 billion tons of CO2 is emitted into the atmosphere from carbon sources, such as burning fossil fuels and tropical deforestation.

Either they include the natural or set forest fire disasters in tropical forests or just did not think of that extra as being pertenent..

New Mars Forums

Announcement

#151 2019-02-09 14:51:23

Re: The Science of Climate Change

#152 2019-02-09 17:36:27

Re: The Science of Climate Change

#153 2019-02-09 17:55:15

Re: The Science of Climate Change

#154 2019-02-09 18:30:11

Re: The Science of Climate Change

#155 2019-02-09 23:17:55

Re: The Science of Climate Change

#156 2019-02-10 10:51:27

Re: The Science of Climate Change

#157 2019-02-10 11:55:56

Re: The Science of Climate Change

#158 2019-02-10 13:50:34

Re: The Science of Climate Change

#159 2019-02-10 14:05:36

Re: The Science of Climate Change

#160 2019-02-10 17:07:09

Re: The Science of Climate Change

#161 2019-02-10 18:10:11

Re: The Science of Climate Change

#162 2019-02-10 20:20:53

Re: The Science of Climate Change

#163 2019-02-10 23:07:55

Re: The Science of Climate Change

#164 2019-02-11 17:26:45

Re: The Science of Climate Change

#165 2019-02-11 18:46:46

Re: The Science of Climate Change

#166 2019-02-11 19:11:38

Re: The Science of Climate Change

#167 2019-02-12 14:04:27

Re: The Science of Climate Change

#168 2019-02-12 18:46:00

Re: The Science of Climate Change

#169 2019-02-12 23:38:07

Re: The Science of Climate Change

#170 2019-02-13 00:18:49

Re: The Science of Climate Change

#171 2019-02-13 03:51:44

Re: The Science of Climate Change

#172 2019-02-13 09:10:45

Re: The Science of Climate Change

#173 2019-02-16 22:34:57

Re: The Science of Climate Change

#174 2019-02-17 18:59:28

Re: The Science of Climate Change

#175 2019-02-18 19:41:19

Re: The Science of Climate Change

Board footer