New Mars Forums
You are not logged in.
- Topics: Active | Unanswered
Announcement
#1 2011-12-01 00:40:45
Reusable Rockets to Orbit
I know that BDBs are in vogue right now as a way to cheapen the journey to orbit significantly, and I think that this is actually a very valid way to go about reducing the costs from where they are today. I know the argument has been advanced before, but in the long term throwing away this expensive technology is just not the way to really drive costs down as far as they can possibly be driven. I am of the opinion that a well-designed reusable rocket could ultimately be every bit as cheap and have every bit as much (or more!) capacity as a space elevator or any form of non-rocket space launch; especially when keeping in mind that early versions of those could well cost every bit as much per kilo as a BDB.
Anyway, I intend to focus on rockets in this post and come up with a plan for a feasible, reusable, and bottom-basement cheap chemically fueled rocket. Because "Man Rating" a rocket is essentially a measure of reliability (Plus keeping g-forces and jerk within reasonable levels, which is generally a result of engineering necessity anyway) and low-cost reusability generally means that the rocket will have to be reused a whole bunch of times, and probably be retired and cannabalized, refurbished, or just plain old sold off afterwards rather than using it to destruction.
So: Reusable rockets. Starting from here, the first basic design choice is fairly simple: How many stages? I would say that reasonable numbers of stages are either one, two, or three, or some hybrid version with drop-tanks and the like. After thinking about it, I am of the belief that a single stage, perhaps with drop tanks but very possibly not is the ideal way to achieve orbit cheaply. My reasons for that are fairly simple in the context of a reusable rocket.
Consider for a second the idea of a reusable two-stage rocket; assume for the moment that there is only one launch complex. Now, your second stage is going to have to make it to orbit so it can just come back to the launch site on the next pass. On the other hand, your first stage will probably end up a good ways downrange. It can certainly be recovered, probably with boats or whatever. The ocean's saltwater and the impact with it will probably cause a significant amount of damage to the craft, and at the very least will hurt its usable lifetime. Therefore, it is logical to instead launch the first stage straight up and have the second stage give the velocity required to attain and maintain orbit; the first stage can then re-enter the atmosphere and land, either horizontally or vertically, and be prepped for its next launch. Right?
Well, only if you have a really freaking big rocket. I know we usually look at the delta-V to orbit as being a scalar state function [neither direction nor the path you take matters]. That is not true. The delta-V to orbit is a vector and is not a state function. It is a vector that is a combination of vertical and horizontal components. The horizontal component is Vorbit, 7800 m/s. The vertical component is a combination of the increase in potential energy, gravity drag (which is separate from potential energy), and air drag, which can be approximated as being primarily vertical because rockets try to get out of the dense lower atmosphere quickly to reduce it, and this involves flying vertically. Doing the reverse vector addition assume that the "scalar" delta V to orbit was 9,400 m/s, I get that the vertical component of this delta V is 5,250 m/s. Therefore this proposal is actually a lot harder than it sounds. The total delta-V in this case would be 13,050 m/s. That's hardly practical. Three stages are subject to similar problems, depending on where you cut the delta-Vs: You either hurt reusability or you end up with huge delta Vs. Possibly both. Drop tanks are subject essentially to the same constraints as TSTO, or else they have to be disposable, which would be far too costly.
Single stage rockets are not subject to any of this. It does not matter that their payload fraction is somewhat lower; due to reusability the per-launch hardware costs will be quite low. Likewise, if we're talking about fuel costs as important factors in the cost of the payload then we are in a cost range that is very favorable.
Of course, questions remain. It's easy to prove that SSTO is possible; many first and second stages are actually entirely capable of launching payload to orbit as a Single-Stage launcher with alterations that are solely related to the fact that they have been repurposed. Reusable is another issue, but I hold that with modern technology it will be possible to create a reusable single-stage to orbit rocket that can be reused a very large number of times (A hundred? A thousand?) and which will result in very minimal per-launch costs. My next post in this thread will address the topic of fuel choice; but what does everyone think so far?
-Josh
Offline
Like button can go here
#2 2011-12-01 01:54:01
- Terraformer
- Member
- From: The Fortunate Isles
- Registered: 2007-08-27
- Posts: 3,988
- Website
Re: Reusable Rockets to Orbit
I think you've gone wrong somewhere, since I seem to recall a proposal (DC-1?) for a TSTO with a pop-up first stage to 100km, and the delta-V was nothing like 5km/s...
Wooo, first post using my swish new Blackberry Torch...
Use what is abundant and build to last
Offline
Like button can go here
#3 2011-12-01 10:32:18
Re: Reusable Rockets to Orbit
It is a vector that is a combination of vertical and horizontal components. The horizontal component is Vorbit, 7800 m/s. The vertical component is a combination of the increase in potential energy, gravity drag (which is separate from potential energy), and air drag, which can be approximated as being primarily vertical because rockets try to get out of the dense lower atmosphere quickly to reduce it, and this involves flying vertically. Doing the reverse vector addition assume that the "scalar" delta V to orbit was 9,400 m/s, I get that the vertical component of this delta V is 5,250 m/s.
I'm guessing your mental image looks something like this:

But in reality you don't get the 9.4 length by adding a 5.25 up leg to a 7.8 sideways leg.
A vertical ascent is done to get above the troposphere as quickly as possible. Typically the vertical ascent takes around 3 minutes.
During vertical ascent, gravity accelerates it down 9.8 meters/second^2. I'll round that to 10 meters/second^2 to make calcs easier.
During 3 minutes of vertical ascent your gravity loss is 180 seconds * 10 meters/sec^2. Which is 1800 meters/sec or 1.8 km/s.
At the top of the vertical ascent rocket speed is usually around zero. When altitude is achieved, the rocket turns sideways for the major horizontal burn.
Hop's [url=http://www.amazon.com/Conic-Sections-Celestial-Mechanics-Coloring/dp/1936037106]Orbital Mechanics Coloring Book[/url] - For kids from kindergarten to college.
Offline
Like button can go here
#4 2011-12-01 14:36:30
Re: Reusable Rockets to Orbit
Terraformer- My answer to that (before reading Hop's post; now I'm definitely going to have to take a much closer look) would be that it probably only went to 100 km, and didn't account for such things as gravity drag while accelerating to orbital velocity, which would be substantial. Further, it only went to 100 km, and not a height at which you could actually orbit, which would generally be more like 200-300 km.
Hop- Your triangle describes my thought process quite accurately. It looks like I need to do some research on what kinds of trajectories are actually usually followed by rockets going for orbit. I did manage to find the following image on Encyclopedia Astronautica:
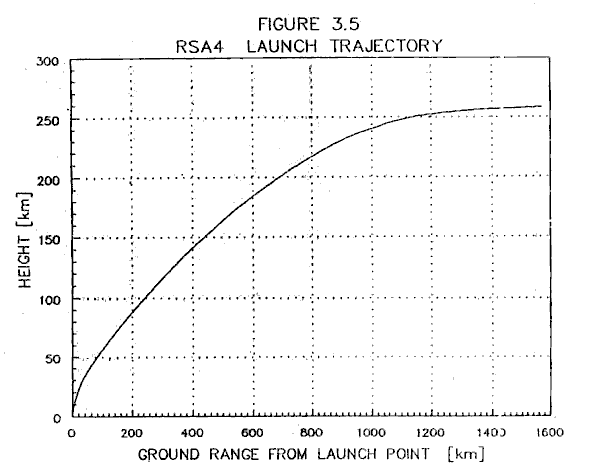
Source: The article on the South African RSA-4 orbital rocket.
Obviously no simple function will be a precise model of the trajectory, but it looks rather like a square root curve until it flattens out up at the top, or perhaps a bit like a circle. That would imply that neither hop's model nor my model of the trajectory is correct; that is to say, (for the RSA 4), it starts off completely vertical and transitions at a relatively constant rate to firing in a more or less completely horizontal manner. Note that by 50 kilometers the rocket already has traveled equal horizontal and vertical distances. I'm going to say, for the sake of argument and reasonable approximation, that all rockets probably have fairly similar trajectories. It's difficult (though probably doable) to say from this graph precisely which direction the rocket is firing, so instead I'm going to do a bit of approximation. Keep in mind that this approximation is reasonable for the sole reason that we know that the value of "9400 m/s" lies somewhere in between two values. These two values are the values of the "get all your vertical delta V out and then all of your horizontal delta V out sequentially" trajectory, which would look like a vertical line followed by a horizontal line (well, approximately) on this graph, and then there's the "do them both at the same time" trajectory, which would look like a beeline to orbit. This is not the best trajectory because you stick around in the lower atmosphere for long time and have to deal with drag and lower Isp and all that nastiness.
I'm going to assume that 9400 m/s is the geometric average of the minimum "beeline" trajectory (⌂Vb) and the maximum "sequential" trajectory (⌂Vs). The mathematical formulation of this would be:
9,400=sqrt(⌂Vb*⌂Vs)
Given that we know that ⌂Vb=sqrt(7800^2+⌂Vvertical^2) and ⌂Vs=7800+⌂Vvertical, we can compute Vvertical to be 2,840 m/s, for a total ⌂Vs=10,640. Still a lot, more than a km/s difference, but granted not as much as I suggested. I still think that a fully reusable SSTO craft is the best answer to the constraints of this problem.
By the way, for those who are interested, I discovered how to do a "⌂" with alt-codes. It's alt+127, I feel like that would be useful to people here.
-Josh
Offline
Like button can go here
#5 2011-12-01 15:07:16
- Terraformer
- Member
- From: The Fortunate Isles
- Registered: 2007-08-27
- Posts: 3,988
- Website
Re: Reusable Rockets to Orbit
Okay, so v^2 = u^2 + 2as, right? Therefore, if we wish to reach 2e5m altitude, we need a velocity of sqrt(2*9.81*2e5), which works out to a smidgen under 2km/s...
Here's the Wiki article for the DH-1 http://en.wikipedia.org/wiki/DH-1.
Use what is abundant and build to last
Offline
Like button can go here
#6 2011-12-01 15:49:18
Re: Reusable Rockets to Orbit
I'm not familiar with your variables, but your answer seems to be of the right order of magnitude. Keep in mind, though, that there are other losses beyond simply increasing the potential energy of the system; note that I put gravity drag and the ⌂V required to reach orbital altitude as different things. Gravity drag is the additional delta V you need when the rocket is accelerating, to keep it in the air. There is of course also air drag.
-Josh
Offline
Like button can go here
#7 2011-12-01 16:15:42
- Terraformer
- Member
- From: The Fortunate Isles
- Registered: 2007-08-27
- Posts: 3,988
- Website
Re: Reusable Rockets to Orbit
Well, certainly, but I note that a well designed ramjet can reach 2km/s, allowing a ramjet first stage to release a high performance upper stage at orbital altitude. If you use aerodynamic lift one your first stage, gravity drag is much less of a problem...
Do you guys not use SUVAT notation in America?
Use what is abundant and build to last
Offline
Like button can go here
#8 2011-12-01 17:58:51
Re: Reusable Rockets to Orbit
... there are other losses beyond simply increasing the potential energy of the system; note that I put gravity drag and the ⌂V required to reach orbital altitude as different things. Gravity drag is the additional delta V you need when the rocket is accelerating, to keep it in the air. There is of course also air drag.
In an airless earth, orbital velocity could be achieved on a horizontal track.
An elliptical orbit with a 0 km altitude perigee (in other words, on earth's surface) would have perigee velocity of 8 km/s and an apogee velocity is 7.64 km/s. .1 km/s suffices to circularize at apogee.
So total delta V budget would be 8.1 km/s for achieving a 300 km altitude circular orbit. A circular orbit at 0 km altitude is 7.9 km/s. So without gravity loss or air drag, the extra expense of a 300 km altitude orbit (vs a 0 km altitude orbit) is .2 km/sec.
In most actual launches, loss from air drag is negligible. Especially if it's a big rocket.
Most of the penalty is gravity drag suffered during vertical ascent.
Hop's [url=http://www.amazon.com/Conic-Sections-Celestial-Mechanics-Coloring/dp/1936037106]Orbital Mechanics Coloring Book[/url] - For kids from kindergarten to college.
Offline
Like button can go here
#9 2011-12-01 18:18:28
Re: Reusable Rockets to Orbit
Do you guys not use SUVAT notation in America?
(Googling...) You just showed me something new.
Hop's [url=http://www.amazon.com/Conic-Sections-Celestial-Mechanics-Coloring/dp/1936037106]Orbital Mechanics Coloring Book[/url] - For kids from kindergarten to college.
Offline
Like button can go here
#10 2011-12-01 19:53:38
Re: Reusable Rockets to Orbit
Terraformer-Ramjets usually don't go straight up. Also, ramjet engines actually have relatively low thrust-to-weight ratios, which makes them less than completely practical. Further, they are not particularly good at going straight up. That's a combination of the combination of thrust-to-weight and the limited distance you have to accelerate. To get to 2 km/s in 50 km, you need to accelerate at an average rate of 40 m/s (T/W ~5, because you have to account for the downward acceleration due to gravity). This is going to be pretty hard to achieve. Especially given that you're going to need another set of engines before you can get your ramjet started.
I would say that it is entirely impractical to use a ramjet as a component of an SSTO rocket, due to the heaviness of the engine and the need to carry additional engines in order to get to orbit. As part of a two-stage launch system, it becomes a more practical consideration. It seems that the peak Isp of a ramjet is around 1200 s, and since we would be operating at velocities that are not the optimal for a ramjet, I would estimate that we could use a working velocity of 950 s. For the 2 km/s boost it would give, it would be necessary to have a mass ratio of 1.25. This is reasonable; however, remembering that you would also need to have some kind of auxiliary engine to get it up to operating speed. This will presumably be either a rocket or a jet engine. Solid rockets are somewhat less than fully reusable (especially for a hundred or a thousand flights) and are rather heavy.
The problem in this case is that the ramjet is highly unlikely to actually be able to fly straight up with a T/W (for the entire rocket, mind you, not just its own stage) of 5. It would probably have to fly horizontally, or at least at an angle. This adds to drag, given that if it were a rocket first stage it would be going straight out of the atmosphere. Further, it has to be moving at 2 km/s at an altitude of (for the sake of argument) 50 km. That's pretty fast to be going in a region of the atmosphere which is still thick enough to be operating a ramjet in. That would necessitate some thermal protection on the upper stage. Given that this stage is still responsible for ~7400 m/s of delta V (perhaps a bit more, given the increase in drag), that's a rather bad choice in engineering terms.
More food for thought: Given that the ramjet is not going to be launching straight up, and since we need to be reusable, it has to get back to the launch site somehow. It can't land just anywhere. Since the launch site is probably going to be somewhere on the western side of the Atlantic, you would have to either land in the ocean (bad), land on the other side of the Atlantic (I would imagine the per-mission shipping costs would be pretty large, therefore bad), or fly back (costs in the ability of your rocket to actually do anything, therefore bad). Plus you have to add two more propulsion systems, which is two more things that can fail, as well as a stage separation, and an engine startup without hold before launch, or any other safety features. I think that the presence of a ramjet booster stage ultimately hurts reliability while at the same time making per-unit costs go up, having an undesirable effect on rocket cost.
Response to Hop coming next.
-Josh
Offline
Like button can go here
#11 2011-12-01 20:15:42
Re: Reusable Rockets to Orbit
Hop- Your calculation for the delta-V required to get from the Earth's surface is simply not correct. Or at least, given the convention of what the delta-V from one point to another is and the context of this discussion your statement that the delta-V from the surface to LEO altitude is .2 km/s (I don't like to say that you are outright wrong when you are not technically incorrect and there is nothing wrong with your math).
This goes back to when I said that delta-V is not a state function: It matters what order you do it in. If you get the tangential velocity first, then yes the delta-V is .2 km/s. If you're launching with an initial speed of zero (as rockets have a tendency to do), then the delta-V is most certainly not .2 km/s It is a matter of potential energy. If you're already moving at 7.9 km/s, an increase in velocity of .2 km/s will result in an increase of energy of 1.6 MJ/kg. To get that increase starting from zero m/s, you need to be moving at 2.4 km/s. This is the real delta-V to that altitude which must be considered by someone designing a rocket.
Air drag is generally not huge, but it's not nothing either. Gravity drag also appears to be relatively small.
-Josh
Offline
Like button can go here
#12 2011-12-01 23:08:01
Re: Reusable Rockets to Orbit
Hop- Your calculation for the delta-V required to get from the Earth's surface is simply not correct. Or at least, given the convention of what the delta-V from one point to another is and the context of this discussion your statement that the delta-V from the surface to LEO altitude is .2 km/s
(I don't like to say that you are outright wrong when you are not technically incorrect and there is nothing wrong with your math).
If you want to try doing the math, a helpful tool is the vis-viva equation:
v^2 = Gm(2/r - 1/a)
G = gravitational constant
m = mass of earth
r = satellite's distance from earth's center
a = semi major axis of orbit.
With that you can determine speed at perigee and apogee of an elliptical orbit.
This goes back to when I said that delta-V is not a state function: It matters what order you do it in. If you get the tangential velocity first, then yes the delta-V is .2 km/s. If you're launching with an initial speed of zero (as rockets have a tendency to do), then the delta-V is most certainly not .2 km/s
Try using the Vis-Viva equation to answer these 4 questions:
What is the velocity of a circular orbit having radius of 6378 kilometers?
Given an elliptical orbit with a 6378 kilometer perigee and an 6678 kilometer apogee,
What is the velocity at perigee?
What is the velocity at apogee?
What is the velocity of a circular orbit having radius of 6678 kilometers?
It is a matter of potential energy. If you're already moving at 7.9 km/s, an increase in velocity of .2 km/s will result in an increase of energy of 1.6 MJ/kg. To get that increase starting from zero m/s, you need to be moving at 2.4 km/s. This is the real delta-V to that altitude which must be considered by someone designing a rocket.
I stipulated the rockets are launched from a horizontal track on an airless world. This exercise is to show what happens when you have zero gravity loss and zero air drag. If you believe I was describing the real delta V someone designing a rocket deals with, you should read more carefully.
Regarding your argument using potential and kinetic energy...
The specific energy (energy per unit mass) of a satellite is
E = v^2/2 - Gm/r
You may recognize the expressions for kinetic as well as potential specific energy.
If you did the 4 vis-viva exercises above, you should have a good idea how to find v.
Given a circular orbit with 6378 kilometers radius, what is E?
Given a circular orbit with 6678 kilometers radius, what is E?
Now take the velocity of the circular orbit with radius 6378 kilometers. Add .18 km/s to this velocity. The object's distance from earth's center is still 6378 kilometers. What is the E of this orbit? How does this E compare to the E of the circular orbit with a radius of 6678 kilometers?
Air drag is generally not huge, but it's not nothing either.
Saturn V had air drag losses of 150 fps. That's about 50 m/s. See page 2 of A Study of Air Launch Methods for RLVs
Gravity drag also appears to be relatively small.
Relative to what? For the Saturn V, gravity loss was about 1500 m/s. This differs from the air drag loss by about a factor or 30.
Last edited by Hop (2011-12-01 23:14:28)
Hop's [url=http://www.amazon.com/Conic-Sections-Celestial-Mechanics-Coloring/dp/1936037106]Orbital Mechanics Coloring Book[/url] - For kids from kindergarten to college.
Offline
Like button can go here
#13 2011-12-02 09:41:00
Re: Reusable Rockets to Orbit
Hop- I am not arguing that your math was done incorrectly. I have full faith in your ability to plug into the vis-viva equation. My argument is that the vis-viva equation is irrelevant in this situation because the rocket does not start off in orbit. As I said before, delta V is not a scalar and not a state function. The delta V required to get to 300 km is different if you're already moving at some velocity. This is more or less basic kinematics. It should be no surprise that the equations governing the behavior of orbiting objects are not relevant when the objects involved are not in orbit.
I estimated before that the actual delta V to orbit is approximately equal (it is my guess that for an intelligently designed trajectory it will actually be somewhat less than this) to the geometric mean of the linear sum of all delta V components and the sum of the components when they are added as vectors. This, I think, accounts for the fact that gravity drag (a quantity that is different from the delta V required to increase your altitude) also tends to be rather large.
It is my understanding that for smaller rockets, the delta V needed to overcome air resistance is generally somewhere between 100 and 200 m/s.
tl;dr: The delta V required to change the height of an orbit is not the same as the delta V to get from the surface to somewhere higher, even when you disregard gravity drag and air resistance .
-Josh
Offline
Like button can go here
#14 2011-12-02 14:40:09
Re: Reusable Rockets to Orbit
Hop- I am not arguing that your math was done incorrectly. I have full faith in your ability to plug into the vis-viva equation. My argument is that the vis-viva equation is irrelevant in this situation because the rocket does not start off in orbit.
You continue to miss my point.
You're trying to assess various factors that add to the delta V for getting to orbit.
We've discussed 1) Air drag, 2) gravity loss, and 3) change of energy for a higher altitude orbit.
Adding .2 km/s to a 6378 km circular orbit would boost it's energy to that of a 6678 km radius circular orbit. This exercise of comparing two circular orbits is to show show something about 3).
As I said before, delta V is not a scalar and not a state function. The delta V required to get to 300 km is different if you're already moving at some velocity. This is more or less basic kinematics. It should be no surprise that the equations governing the behavior of orbiting objects are not relevant when the objects involved are not in orbit.
Revisiting the horizontal launch track on an airless earth. In such a scenario payloads could be launched with virtually no gravity loss and no air drag loss.
Starting from velocity = 0, 7.9 km/s would suffice to put an object in a 6378 km radius low circular orbit.
Starting from velocity = 0, 8.1 km/s would suffice to put an object in a 6678 km radius low circular orbit.
I estimated before that the actual delta V to orbit is approximately equal (it is my guess that for an intelligently designed trajectory it will actually be somewhat less than this) to the geometric mean of the linear sum of all delta V components and the sum of the components when they are added as vectors.
The acceleration lost to gravity over time doesn't give you a vertical velocity vector whose foot you can place on the head of a horizontal vector to give you a 9.4 km/s hypotenuse. This wrong model is what gave you 5.25 km/s to get above the atmosphere.
Last edited by Hop (2011-12-02 14:40:39)
Hop's [url=http://www.amazon.com/Conic-Sections-Celestial-Mechanics-Coloring/dp/1936037106]Orbital Mechanics Coloring Book[/url] - For kids from kindergarten to college.
Offline
Like button can go here
#15 2011-12-05 01:44:43
Re: Reusable Rockets to Orbit
Hop-
I understand your point perfectly. My problem with your point is that it is not right, not that I don't get it.
Consider for a second what you are doing: You are using the equations governing the behavior of a body that is in orbit to predict the behavior of a body that is not in orbit. That should be a red flag.
I already conceded that a simple vector addition does not work to calculate the orbital velocity from components. From that, however, I did some research and pulled up the trajectory that one rocket takes to orbit. As we saw, it was neither the (theoretical, though not actual) minimum where you could use vector addition of the components to obtain the delta-V. However, at the same time, by looking at the graph, you can tell that it's not the result of the additive trajectory, as that would result in a different shaped line than the one you see (I trust you can evaluate the relevant parametric equations and compare the curve produced to the one in the graph, you will see that they are far from the same. Therefore, I conclude that the actual delta-V must be somewhere between those values. I decided, for no particular reason other than it gives a good average value, to use the geometric average of those two values. This is not mathematically rigorous, but given that we don't know (and I at least do not have the time to calculate) the optimum trajectory for a rocket launching to orbit, this seems reasonable.
Mathematically, this would be written:
⌂Vb=sqrt(⌂Vv^2+⌂Vh^2)
⌂Vs=⌂Vv+⌂Vh
⌂V=sqrt(⌂Vs*⌂Vb)
Where ⌂Vb is the ⌂V if you were to calculate it as a sum of vector components, ⌂Vs is the ⌂V if you were to calculate it as a sum of scalar components, ⌂Vv is the linear sum of the vertical components, ⌂Vh is the linear sum of the horizontal components.
If you look at the trajectory graph that I posted, it is clear that at least some of the time the rocket is firing its engines in a direction other than vertical or horizontal. Therefore, there are elements both of vector addition and linear addition of vector components.
I'm not quite sure I can explain this any better than to repeat myself in saying that ⌂V is not a scalar and is not a state function. Energy, on the other hand, is. To go from the surface of the Earth to 300 km requires an input of 2.94 MJ/kg. The force for this energy ha to be applied straight up. Therefore, as per implicit convention, we use the equation Esp=.5*v^2 where Esp is in J/kg to calculate a velocity of 2,425 m/s (It will actually be slightly less than this because I did not account for the difference in gravity between . If you do the energy calculations, the difference in energy between 8.1 km/s and 7.1 km/s is very similar to that number (though given that there is a very limited number of sig-figs here there is a significant margin of error).
Even though we're not doing pure vector addition, it is still correct to speak of the individual parts as components because there is an element of vector addition. The component, in this case is 2,425 m/s (or more realistically, something like 2,300 m/s). This does not add linearly into the final delta V.
Last edited by JoshNH4H (2011-12-05 01:45:34)
-Josh
Offline
Like button can go here
#16 2011-12-05 11:12:13
Re: Reusable Rockets to Orbit
I'm not quite sure I can explain this any better than to repeat myself in saying that ⌂V is not a scalar and is not a state function. Energy, on the other hand, is. To go from the surface of the Earth to 300 km requires an input of 2.94 MJ/kg.
This from potential energy?. I get 2.81 MJ/kg.
The force for this energy ha to be applied straight up. Therefore, as per implicit convention, we use the equation Esp=.5*v^2 where Esp is in J/kg to calculate a velocity of 2,425 m/s (It will actually be slightly less than this because I did not account for the difference in gravity between . If you do the energy calculations, the difference in energy between 8.1 km/s and 7.1 km/s is very similar to that number (though given that there is a very limited number of sig-figs here there is a significant margin of error).
((8100 meters/second)^2) / 2 = 32805000 (meters/second)^2
((7100 meters/second)^2) / 2 = 25205000 (meters/second)^2
32805000 - 25205000 = 7600000
The specific energy difference between 8.1 km/s and 7.1 km/s is 7.6 MJ/kg. Not remotely similar to 2.94 MJ/kg.
I don't know where you got 7.1 km/s, though.
The specific energy difference between 7.9 km/s and 8.1 km/s is 1.6 MJ/kg. Also not remotely similar to 2.94 MJ/kg.
I don't have time to look at your math. Your approach seems to be to look at the numbers and then try to guess an equation that will give an answer that matches. When you derive your equations from first principles, I will give them more attention.
Hop's [url=http://www.amazon.com/Conic-Sections-Celestial-Mechanics-Coloring/dp/1936037106]Orbital Mechanics Coloring Book[/url] - For kids from kindergarten to college.
Offline
Like button can go here
#17 2011-12-05 21:59:00
- SpaceNut
- Administrator
- From: New Hampshire
- Registered: 2004-07-22
- Posts: 29,920
Re: Reusable Rockets to Orbit
http://en.wikipedia.org/wiki/Rocket_equation
basic principle of a rocket: where a device that can apply acceleration to itself (a thrust) by expelling part of its mass with high speed and moving due to the conservation of momentum. Specifically, it is a mathematical equation that relates the delta-v (the maximum change of speed of the rocket if no other external forces act) with the effective exhaust velocity and the initial and final mass of a rocket (or other reaction engine.)
For any such maneuver (or journey involving a number of such maneuvers):
where:m0 is the initial total mass, including propellant.
m1 is the final total mass.
ve is the effective exhaust velocity. ( where Isp is the specific impulse expressed as a time period)
is delta-v- the maximum change of speed of the vehicle (with no external forces acting)
Units used for mass or velocity do not matter as long as they are consistent.
http://en.wikipedia.org/wiki/Delta-v
Delta-v is produced by the use of propellant by reaction engines to produce a thrust that accelerates the vehicle.
where
T is the instantaneous thrust
m is the instantaneous mass
If there are no other external forces than gravity, this is the integral of the magnitude of the g-force.In the absence of external forces, and when thrust is applied in a constant direction this simplifies to:
which is simply the magnitude of the change in velocity. However, this relation does not hold in the general case: If, for instance, a constant, unidirectional acceleration is reversed after (t1 − t0) / 2 then the velocity difference is v1 − v0 = 0, but delta-v is the same as for the non-reversed thrust.
Not sure what part of the problem is missing.
The rockets exhaust is the force and that is not a constant as in F=MA nor is the consumption rate that changes the mass of the rocket along the path to orbit.
Offline
Like button can go here
#18 2011-12-05 22:06:16
- GW Johnson
- Member
- From: McGregor, Texas USA
- Registered: 2011-12-04
- Posts: 6,108
- Website
Re: Reusable Rockets to Orbit
Hi gang:
This is GW Johnson the old aero engineer, and ramjet expert from long ago. I surely am glad to see the forums up and running again.
In recent news: I have picked up a consulting client for a possible ramjet launch effort. And, that client and I both think I may be just about the last living US all-around expert in ram propulsion (I seem to have outlived the rest).
I’m particularly glad to see LEO access under active discussion, especially with Josh and Hop talking about reusable vehicles, and perhaps ramjet assist. The last stuff I had is a posting over at http://exrocketman.blogspot.com, where I looked at horizontal takeoff and landing with a winged first stage using separate rocket and ramjet power. That article is dated August 22, 2010, so it’s way down the list (chronological, latest on top). There’s a navigation tool by date and title on the left, under my photo. It looked to me like a staging condition of near Mach 6 at around 60,000 feet altitude might well work out, including booster flyback. And, it looks like ramjet might really pay off in this scenario.
Josh is exactly right: the frontal thrust density of ramjet is too low to support vertical acceleration of a heavily-loaded vertical launch vehicle on ramjet alone. But parallel-burn of otherwise-separate rocket and ramjet might offload some of the thrust requirement temporarily onto the higher-Isp ramjet, thus swapping a smidge of rocket propellant for a smidge of extra payload. That kind of vehicle is moving only around M2 at 60,000 feet, so it’s a “low-speed” pitot inlet design, not the “high-speed” spike inlet that makes sense for the ramjet launch airplane. Whether this idea is actually technically and economically attractive in vertical launch, remains to be seen. I just dunno, yet.
You can think of “high-speed” systems being some sort of spike or ramp inlet, a dump combustor, and a very mild-expansion convergent-divergent nozzle. Min Mach number is around 1.5, and max is around M5 to 6, depending more on vehicle drag than the ramjet design itself. I looked at nose inlets, but side inlets also work. Peak performance is around M2 to 3, and frontal thrust density falls too low to provide effective acceleration above about 60,000 feet. It doesn’t matter a lot whether you analyze RP-1 or JP-5 kerosene, or even RJ-5/Shelldyne-H synthetic, they all come out similar in proportions and performance. I think liquid methane would look very similar to kerosene, too.
“Low speed” systems are a simple pitot (normal-shock) inlet, most likely a nose inlet, a dump combustor, and a convergent-only nozzle. Min Mach is a tad fuzzy, there being thrust greater than drag (in low-drag nacelles) down under Mach 0.5, although Isp is over kero-lox rocket levels only above around Mach 0.7-ish. Max Mach is around 2 to 3, depending more on vehicle drag than the ramjet, with max performance around M1.5 to 2. I think thrust densities fall too low to be useful for acceleration above around 60,000 feet, although this remains to be seen for sure. Again, specific fuel choice is not all that important.
Whatever I do come up with, I’ll let y’all know. This stuff is fun. I haven’t done any of it in almost 2 decades, now. I think I’ll turn my old how-to notebooks into a published book. Otherwise, the art will die with me. (It’s still mostly art, until I can get it all written down). That ain’t easy.
GW
GW Johnson
McGregor, Texas
"There is nothing as expensive as a dead crew, especially one dead from a bad management decision"
Offline
Like button can go here
#19 2011-12-06 01:07:34
Re: Reusable Rockets to Orbit
So: I promised an analysis of the fuels involved in my hypothetical space rocket. There are two basic schools of thought on this- there's the school of thought suggesting that dense, somewhat lower Isp propellants are advisable; on the other hand, there are also people who think that we should just bluntly attack the problem by raising Isp as high as possible to minimize the mass ratio.
This represents two different ways of looking at the issue, which are best described with two different figures of merit. The "dense propellants are better" school will tend to point at a figure of merit that is something like "Mass Ratio/Density of propellant," which is essentially a measure of how much tank volume you will need for the fuel needed to get to orbit. This can be calculated by using the Rocket equation, Rm=e^(⌂V/Vex), and dividing by the density (I use g/cm^3; even though it's not metric, it gives numbers that are of very pleasing orders of magnitude, for chemical propellants that could reasonably be proposed between 5 and 50). The second is Mass ratio, which more simply gives the ratio of mass when fully fueled ("Wet" Mass) to the mass when completely empty ("Dry" Mass). The following is a table of a few different propellants and certain properties. [For those who don't know, Isp is Exhaust Velocity (Vex) divided by g, 9.8 m/s^2]

Most of the fuels in this table are relatively standard, with a couple exceptions. ALICE is Aluminium-Ice propellant. There's not much out there, but you can see this website for more information. Alox is Aluminium-Oxygen, in the form of a monopropellant suspension. Like ALICE, little research has been done, though that which exists can be found on the website for Wickman Space. HDA stands for "High Density Acid," a 50/50 by mass mixture of Dinitrogen Tetroxide and Nitric Acid which provides the highest density. I've seen densities of 1.66 g/cc, but I assumed 1.60 g/cc. The Isp of AlOx and especially ALICE is very poorly constrained. I've seen sources suggesting Vacuum Isps of 285 s for AlOx, though my calculations tend to show more like 200 s. I have not seen Isp figures for ALICE at all, but it was suggested that it would be better than traditional solid rockets, which tend to perform in the region of 270 s. 280 s is a complete guess, and it seems to me an optimistic one at that. It's there more for comparison purposes, given that I cannot reasonably incorporate into a rocket design a fuel whose Isp I can only guess at.
Assuming for the moment that these are our only practical choices for rocket fuels, it's tempting to just go with methlox for having the best all-around combination of mass ratio and MR/D. However, just because these are (for the sake of argument, though if I've missed any, by all means) our only propellant choices does not mean that we're actually totally limited to the performance values seen here.
Let me explain: Say you have a rocket burning two different propellant combinations in two entirely separate rocket engines. The effective exhaust velocity will be a weighted average of the two exhaust velocities based on the force from each engine. Because Mass Ratio is an exponential function of the inverse of Vex, small increases in exhaust velocity cause more significant decreases in the Mass Ratio. Meanwhile, because the lower Vex fuels generally have a higher density, combining a high-density medium to low Isp fuel with something like H2/LOX can result in significant benefits, depending how important MR/D is to you compared to MR. Below is a table of various combinations of fuels and their performance values, optimized for lowest MR/D.

Of fuels that I could actually reasonably endorse the use of at this time (eg, fuels not involving Alox or ALICE), kero/HDA-H2/LOX has the best MR/D and H2/LOX obviously has the best mass ratio. Depending on the relative importance you place on mass ratio vs. MR/D, different fuels will be optimum. I actually really like the combination of Kerosene/HDA and H2/LOX as a fuel because it seems to me that it strikes a good balance between low volume and low mass.
-Josh
Offline
Like button can go here
#20 2011-12-06 01:20:00
Re: Reusable Rockets to Orbit
JoshNH4H wrote:I'm not quite sure I can explain this any better than to repeat myself in saying that ⌂V is not a scalar and is not a state function. Energy, on the other hand, is. To go from the surface of the Earth to 300 km requires an input of 2.94 MJ/kg.
This from potential energy?. I get 2.81 MJ/kg.
I was estimating by holding gravity constant, which is close enough to true over 300 km that I got a reasonably accurate answer, in this case within 5%.
JoshNH4H wrote:The force for this energy ha to be applied straight up. Therefore, as per implicit convention, we use the equation Esp=.5*v^2 where Esp is in J/kg to calculate a velocity of 2,425 m/s (It will actually be slightly less than this because I did not account for the difference in gravity between . If you do the energy calculations, the difference in energy between 8.1 km/s and 7.1 km/s is very similar to that number (though given that there is a very limited number of sig-figs here there is a significant margin of error).
((8100 meters/second)^2) / 2 = 32805000 (meters/second)^2
((7100 meters/second)^2) / 2 = 25205000 (meters/second)^232805000 - 25205000 = 7600000
The specific energy difference between 8.1 km/s and 7.1 km/s is 7.6 MJ/kg. Not remotely similar to 2.94 MJ/kg.
I don't know where you got 7.1 km/s, though.
The specific energy difference between 7.9 km/s and 8.1 km/s is 1.6 MJ/kg. Also not remotely similar to 2.94 MJ/kg.
7100 m/s was a typo, my mistake. I suppose this shows another rather important difference between your number any my number: your number includes a change in orbital speed (e.g., a horizontal component) while mine does not.
I don't have time to look at your math.
I would much prefer to wait a few days for a substantive reply if one would be forthcoming. If, on the other hand, you are not willing to consider my points, I'm not quite sure what you're doing.
Your approach seems to be to look at the numbers and then try to guess an equation that will give an answer that matches. When you derive your equations from first principles, I will give them more attention.
That's an incredibly dismissive way to talk about the scientific method. The simple fact is that launching to orbit involves a lot of very complex phenomena, which makes deriving from "first" principles impractical, and empirical models a much better way to deal with the complexities of the situation. I don't doubt that you know your stuff when it comes to orbits which can be modeled with classical Newtonian gravitation. Launching from Earth's surface to LEO involves a significant number of factors which simply do not fit into that category.
-Josh
Offline
Like button can go here
#21 2011-12-06 01:46:06
Re: Reusable Rockets to Orbit
GW- What would your response be to my suggestion that given the somewhat limited range over which it could actually add to delta-V, as well as the need for flyback, and the significant per-launch costs of integrating another stage each launch, the costs of a ramjet boost may outweigh the benefits? Seeing as you're quite familiar with this technology (and that seems to be a massive understatement), it would be quite foolish to make that judgment without at least asking you.
Also, as a longtime engineer, what do you think of my model for analyzing the parts of the delta V required to get to orbit? I describe it on the post with the trajectory graph.
Also, good luck with your textbook. Perhaps one of these days required reading for one of my classes will be a textbook with your name on it.
-Josh
Offline
Like button can go here
#22 2011-12-06 04:29:04
- Terraformer
- Member
- From: The Fortunate Isles
- Registered: 2007-08-27
- Posts: 3,988
- Website
Re: Reusable Rockets to Orbit
Welcome back, GW. It's a pity all the threads are gone that had a lot of good discussions about Ramjets.
What are the possibilities for a turbojet-ramjet craft with two sets of engines? They would presumably remove the need for a rocket to boost it up to ramjet operating speed, and allow it to fly back under its own power (though it may be able to glide back anyway).
I'd go with the same fuel used in the rocket, to simplify matters.
Use what is abundant and build to last
Offline
Like button can go here
#23 2011-12-06 07:16:35
Re: Reusable Rockets to Orbit
7100 m/s was a typo, my mistake.
You admit this mistake and then ignore the correct numbers.
Again, the difference between 8.1 and 7.9 km/s is 1.6 MJ/kg.
This is NOT the same as the potential energy difference between earth's surface and a 300 km altitude, 2.81 MJ/kg.
That's an incredibly dismissive way to talk about the scientific method.
You're trying (unsuccessfully) to get the numbers to meet your expectations.
This is not the scientific method.
I find it incredibly arrogant that you characterize dismissal of your models as dismissing the scientific method.
Last edited by Hop (2011-12-06 07:30:37)
Hop's [url=http://www.amazon.com/Conic-Sections-Celestial-Mechanics-Coloring/dp/1936037106]Orbital Mechanics Coloring Book[/url] - For kids from kindergarten to college.
Offline
Like button can go here
#24 2011-12-06 07:28:22
Re: Reusable Rockets to Orbit
So: I promised an analysis of the fuels involved in my hypothetical space rocket. There are two basic schools of thought on this- there's the school of thought suggesting that dense, somewhat lower Isp propellants are advisable; on the other hand, there are also people who think that we should just bluntly attack the problem by raising Isp as high as possible to minimize the mass ratio.
This represents two different ways of looking at the issue, which are best described with two different figures of merit. The "dense propellants are better" school will tend to point at a figure of merit that is something like "Mass Ratio/Density of propellant,"
Higher ISP propellants have lower thrust.
If you have anemic thrust, it will take you longer to achieve altitude and you thus incur greater gravity losses.
An example is ion engines. Very good ISP. But T/W < 1. It would take forever to reach altitude and gravity loss would be infinite.
But since you're predisposed to thinking gravity loss is inconsequential, you likely won't consider consider stuff like thrust to weight ratio.
Hop's [url=http://www.amazon.com/Conic-Sections-Celestial-Mechanics-Coloring/dp/1936037106]Orbital Mechanics Coloring Book[/url] - For kids from kindergarten to college.
Offline
Like button can go here
#25 2011-12-06 07:44:28
Re: Reusable Rockets to Orbit
Welcome back, GW. It's a pity all the threads are gone that had a lot of good discussions about Ramjets.
Nasaspaceflight.com has numerous threads on related topics. If you use search strings like ramjets, scramjets, Skylon, you will find many discussions.
One such discussion is The airbreathing space launch thread.
Hop's [url=http://www.amazon.com/Conic-Sections-Celestial-Mechanics-Coloring/dp/1936037106]Orbital Mechanics Coloring Book[/url] - For kids from kindergarten to college.
Offline
Like button can go here