
https://usafacts.org/issues/climate/sta … hampshire/
recent image from the rain
current radar map
Climeworks' direct-air-capture plant can remove up to 36,000 metric tons of carbon from the air a year.
]]>Why the climate doom-mongers are always wrong
spiked
92.7K subscribersSubscribe
And this: https://www.youtube.com/watch?v=tqcDyHdbYd4
This one describes a "Climate Religion"
Done
]]>https://www.euronews.com/green/2024/02/ … ing-planet
to monitor natural and pollution events on the planet, it unfortunately is political at times
and sometimes US congressman would cite Bible 'evidence', stories of Noah, his religion tale of animals on the ship and biblical flood story and a promise of rainbows using the Bible writings to dispute human link to climate change
Fort Worth Star-Telegram urged that Barton not seek re-election Tim O'Hare, the Chairman of the Tarrant County Republican Party, called on Barton "to not seek re-election and to retire from Congress" saying he is guilty of "sexual immorality".
Barton accused the Obama administration of a "$20 billion shakedown" of oil giant BP after the company reached an agreement with the administration to establish an escrow account to pay the claims of people harmed by the Deepwater Horizon oil spill
Joe Barton voted against Hurricane Harvey relief, he liked open borders and illegal entry if the person could become American, Barton called on the House leadership to pass naturalization legislation for children who came across the border illegally with their parents, Joe Barton liked other sins and vices and has sought to permit online poker, and regulate it on a federal level.
Climate scientist Michael Mann wins defamation case against conservative writers
]]>The issue is that there's no differentiating "the weather" from "the climate". We're still talking about the exact same thing over different periods of time. We lack the ability to accurately predict the weather more than a week in advance, ergo our ability to accurately predict weather over decades to centuries is nonexistent. Within the field of statistics, as you attempt to predict further and further into the future, all forecasting errors magnify over time. That means the overall accuracy of your predictions decreases over greater and greater periods of time. This is Statistics 101, as taught in virtually any college, anywhere on the planet. We can produce an estimate of what we think the range of probable values are, but even that will be hampered by our limited predictive accuracy.
Asserting that you know with certainty what the weather will be like, over decades to centuries, is tantamount to outright lying. The very best you can hope to do is to account for and control for all input variables, and then you end up with a confidence interval for your predicted values (stock prices, total number of new cars sold, mean surface temperatures, etc).
Since there's no freak-out over the fact that "the temperature" changes by 20+ degrees, every single day, why is there a freak-out over the temperature changing by fractions of a single degree over decades?
Stating silly obvious things like "climate change is real", "climate change is happening now", or "climate change is the greatest threat to humanity", is exactly like saying "day and night is real", "the weather is changing right now", or "when it heats up during the day or gets colder at night, that's the greatest threat to humanity". Well... It was some 30 degrees warmer during the day here in Houston than the coldest it was at night. Nobody or almost nobody died as a result. If you were going to freak out about something, then why not freak out over the fact that it was about 30 degrees warmer at sunset than at sunrise?
There was no point in time during the past when mean surface temperatures, precipitation levels or patterns, mean sea level altitude, ocean tides, vegetation, or any other aspect of the natural world remained fixed and unchanging. Whether anyone was paying attention to or recording the changes or not, they were always taking place. The natural world was always been in a state of constant flux and it always will be.
Rather than biting my nails over the fact that the natural world always changes, I choose to respond such that those changes don't completely upend or outright end my life. If it's cold outside, I put a jacket and pants on. If it's hot, I wear a T-shirt and shorts. If it rains, I stay indoors or carry an umbrella. If I find myself in a radically different environment like the ocean, then I learn how to swim and take a life jacket that floats well. If it floods, I move to higher ground, either on my feet or in a vehicle. My adaptability to my current environment is why I'm still alive and well after 40+ years. Most other plants and animals, at least the ones which haven't already gone extinct, do the exact same thing.
]]>Weather is highly variable and unpredictable. Figuring out what can be considered "normal" or typical depends greatly upon what length of time you look at. Over large enough periods of time, what you will note is very dramatic swings in weather and precipitation.
There were record high temperatures in New Hampshire in the late 1800s and across most of the US during the 1930s. Given how ridiculously short the period of time has been over which we had accurate direct observation of large areas of the planet, jumping to immediate worst-case conclusions was and is an absurdity.
Actual scientists, as opposed to political activists with science degrees, have far more measured commentary on what happened, why it most likely happened, and what the limits are of our ability to accurately predict weather phenomenon. Their comments tend to be none-too-exciting or over-the-top about anything they're witnessing, mostly because it's something they've all seen before, so becoming overly excited about it wouldn't serve any public interest.
Given the plainly stated fact from our meteorologists that our predictive capability regarding weather is basically garbage when we attempt to predict the weather more than a week into the future, what on Earth makes us think we can predict weather 50, 100, or 200 years into the future?
Climate is merely weather over time. We arbitrarily define it as weather over 30 years. I've never seen a good argument as to why it's defined that way, because Earth and the entire rest of the universe doesn't operate over 30 year time periods. Fully developed human brains can conceptualize how long that is, but even 30 years (half to a third of a human lifetime) holds different significance for different people. As animated as leftists become over the weather, short-term radical weather shifts are very few and far between.
Leftism's latest "weather scare" is a bit like getting amped up about the price of real estate. Over enough time, the price of real estate always goes up, which is why everyone says it's generally a good investment and the primary way inter-generational wealth is created. Sometimes it goes up a lot, sometimes only a little, but the direction it's headed in isn't very debatable or contentious unless you're trying to manipulate people into behaving in a way that benefits you or your company.
I'm not dumb. I can see weather changes over time. I can see that things are getting a little bit warmer. I'm not freaked out about it, though, because it was changing since the Earth was formed and will continue to do so long after I'm gone and my children are gone.
All catastrophes and emergencies are very rapid destructive events that happen over seconds to perhaps weeks at most. Whenever a dam breaks, the water does the damage in minutes to hours. Humanity may spend months or even years cleaning up after that, but the actual emergency is already over before much of anything meaningful can be done about it. When you know something is coming and you can't do much of anything meaningful to stop it, then you start mitigating the damage or risk that likely event poses to your people by preparing for that eventuality. At the very least, that's what you do in the military. Ships can sink, so you teach sailors how to swim. You don't teach sailors to be terrified of the ocean. Murphy's Law states that anything that can happen, will happen. The corollary to Murphy's Law, is that since you know Murphy was an optimist, you prepare the battlefield to achieve the most favorable outcome with the minimum loss of life.
Why is there so very little emphasis placed on recycling a substance as endlessly recyclable as CO2?
It should be painfully clear by this point that humanity requires on-demand energy production and easy storability for its primary energy systems, in order to function as it presently does. Gasoline, diesel, kerosene, Uranium, and Thorium beat the snot out of all competing technologies when it comes to all the properties that make them good at producing or storing energy. The fact that there's some waste product involved is of lesser importance than what we do with that waste product. We have the technology to do that, we're simply choosing not to use it, which makes very little sense from a holistic perspective.
At the present time, we're running around with our hair on fire, pretending that we're going to stop using the most dense forms of stored energy while we make radical and incredibly energy-intensive changes to every aspect of how we live in modern industrialized societies. Both courses of action are wildly practical and thoroughly unhelpful.
]]>Yes, animals and most plants do not fare well with it being to hot or to cold for sure and that is why man has learned how to control its environment such as in a greenhouse.
We are still debating the effects and cause for the grand swing in temperatures. The ice only captured co2 but that is not all that caused the swing and we know this.
]]>Normal is a subject that's beholden to everyone's personal normalcy bias.
Earth was much warmer and wetter over a very large portion of its entire history, in comparison to the past 100 years that everyone is so fixated on. Scientists have repeatedly stated that Earth's biodiversity was at an all-time high during that period of time. If we return to that epoch of Earth's history, rather than "Snowball Earth", it wouldn't be the worst thing that's ever happened.
Most plant and animal life flourishes in warmth, but nearly goes extinct in cold. There are drastically fewer species of plants and animals in Antarctica than in South America. Throughout all of Earth's history, the planet itself didn't care one little bit if one species went extinct while new ones were created and thrived. The only constant was change. Species either adapted or died out. There was no statement of morality attached to that reality, either, until human higher cognitive function came along. It was not perceived as "good" or "bad", it just was.
Over time, life processes extracted so much Carbon from the environment that Earth swung between "full snowball" and "partial snowball". Unwittingly, humanity came along and, through use of stored hydrocarbon energy reserves, purchased another hundred million years of survivable temperatures for most of the life here on Earth. This was not done without a cost to ourselves or environment, but the alternative was all life being snuffed out as plants died off from CO2 starvation. We did a good thing by accident, that happened to provide great benefits to us at the same time, which is probably how and why we did it. We restored balance to "The Force", which doesn't mean "everything is peaches and cream" or "there are no consequences for doing so". If we lived on a mostly desert-like planet but by happy accident unlocked vast stored reserves of liquid water, then yes, some part of the desert would be lost during that process, but overall life improved over time, because it had more opportunity to grow.
]]>You were complaining about how cold it was a few years back and that your family had trouble staying warm during the winter.
Is it vitally necessary to have feet of snow on the ground for you to live in New Hampshire, or do you appreciate not being barricaded in your own home or sliding across ice and snow-covered streets while driving to work?
]]>
https://usafacts.org/issues/climate/sta … hampshire/
recent image from the rain
current radar map
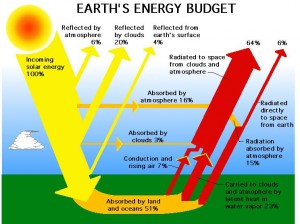
The Earth receives 174 petawatts (PW) of incoming solar radiation (insolation) at the upper atmosphere. Approximately 30% is reflected back to space while the rest, 122 PW, is absorbed by clouds, oceans and land masses. The spectrum of solar light at the Earth's surface is mostly spread across the visible and near-infrared ranges with a small part in the near-ultraviolet. Most of the world's population live in areas with insolation levels of 150–300 watts/m2, or 3.5–7.0 kWh/m2 per day
Since earths radius is not changing but the hours are which means the amount of energy that earth is absorbing is going to rise. It is not manmade, but we are not helping with creating more gasses that hold energy longer.
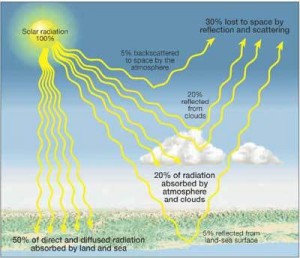
Sun energy, or solar radiation, is the energy that reaches the Earth from the Sun. About 71% of the sun energy that reaches the Earth is absorbed by its surface and atmosphere.
The rest is reflected back to space by clouds and Earth's surface. The absorbed energy causes the molecules of the object or surface it strikes to vibrate faster, increasing its temperature.
The energy is then re-radiated by the Earth as longwave, infrared radiation, also known as heat. Some of the Sun’s energy reaches Earth in the form ultraviolet (or UV) radiation.
Fortunately, the ozone layer high in Earth’s atmosphere absorbs a lot of this UV radiation and blocks it from reaching Earth’s surface.
Gravity from the Moon doesn't just cause tides in the ocean. It also causes tides in the crust. Remember the crust is 3 to 43 miles (4.8 to 69km) thick. Mostly 4-6 miles (7 to 10km) under the ocean, mostly 22 miles (35km) under continents. This is a planet 12,750km diameter. It's mostly mantle, which is soft like plasticine. When pressure is reduced, mantle becomes magma, but it's mostly soft. Tides of the crust move slowly, causing a bulge toward the Moon, and a matching bulge on the opposite side of the Earth. Those bulges move slow, so lag behind direct alignment. Behind in time, just past direct alignment in space. The Moon's gravity pulls on that bulge causing Earth's rotation to slow.
]]>